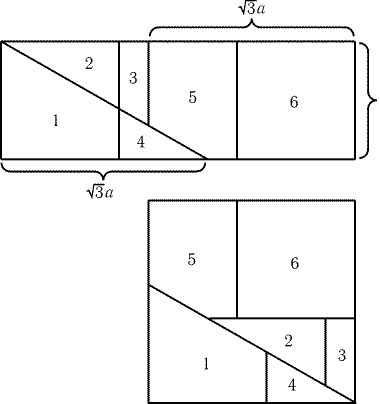
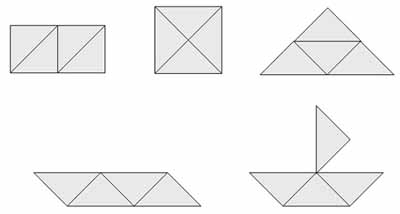
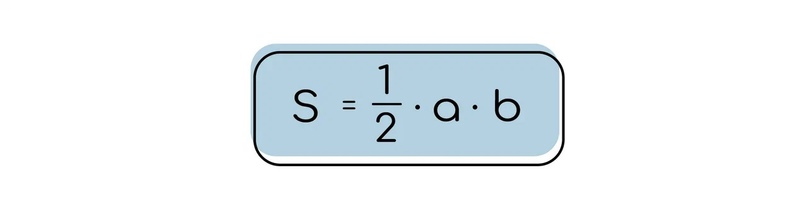Как из 4 треугольников сделать прямоугольник

Разбить квадрат на равнобедренные треугольники. Вот, наткнулся в сети на: задачу в стихах. Но, думается, общественности это на один укус если ещё не проходила такая задча -- Задачка по планиметрии Мишаня Дундило Математики в прошлом задачи в стихах излагали.

Разбиение на подобные треугольники

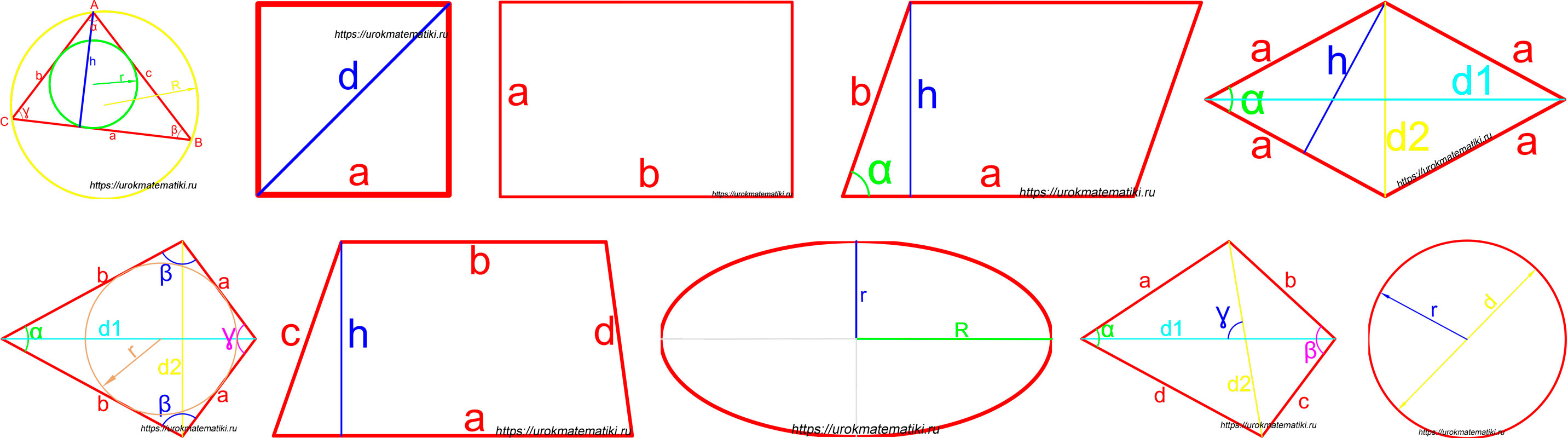
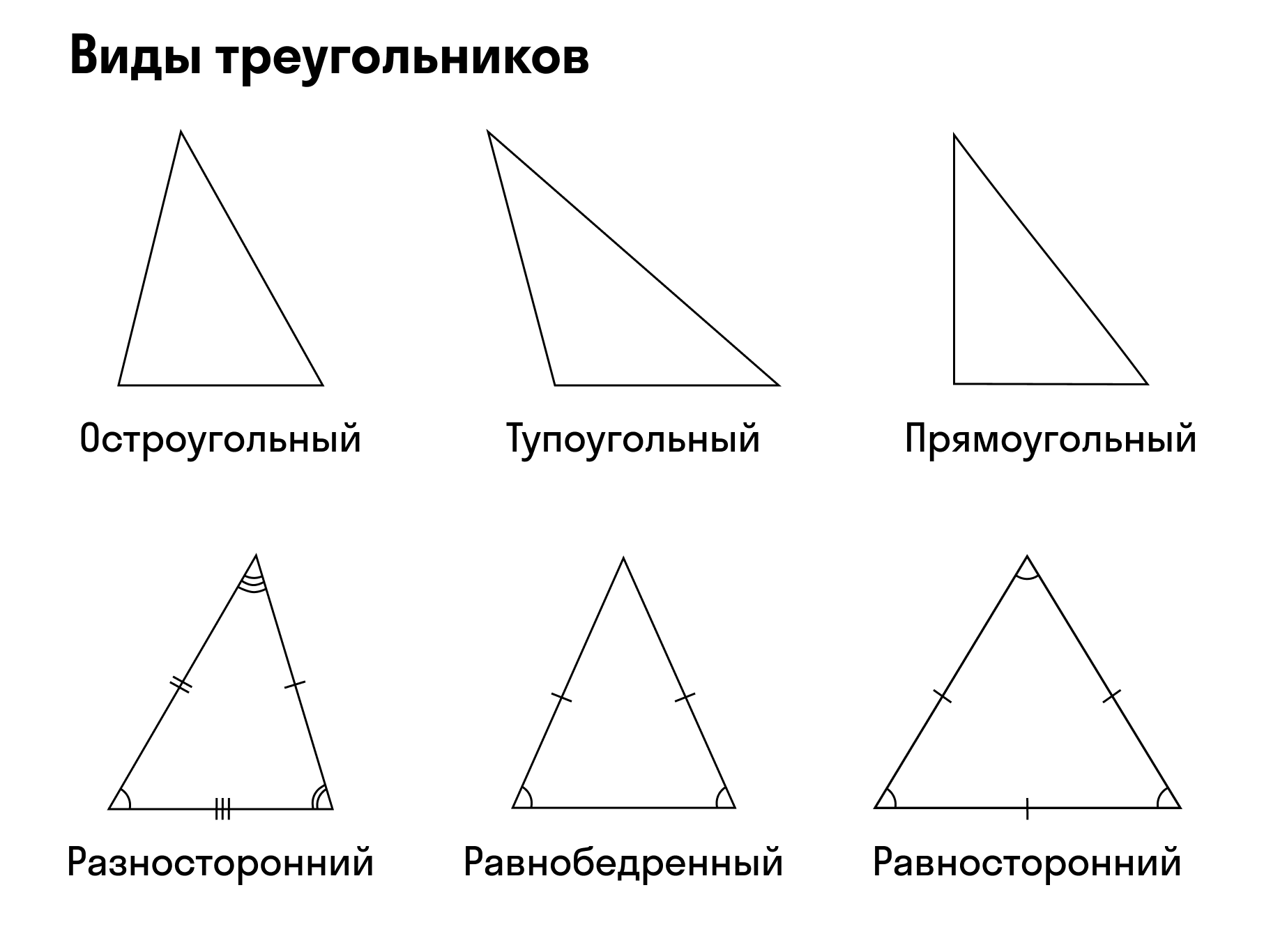
Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. Внутренние углы имеют соотношение 1 : 1 : 2. Боковые стороны являются катетами , основание — гипотенузой. Высота , опущенная на гипотенузу, равна её половине:. Периметр равнобедренного прямоугольного треугольника равен.

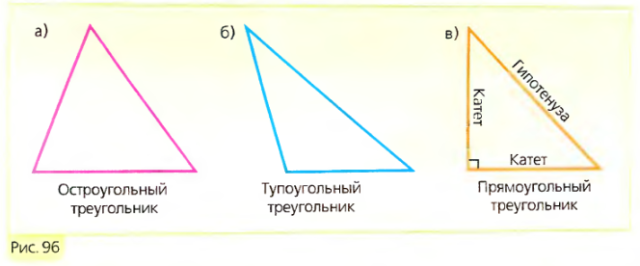
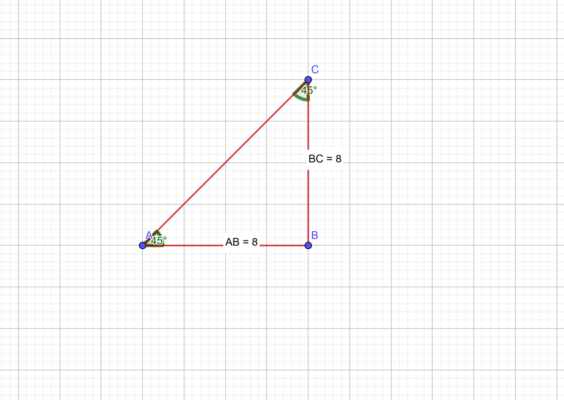
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии. Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме: [ 1 ].

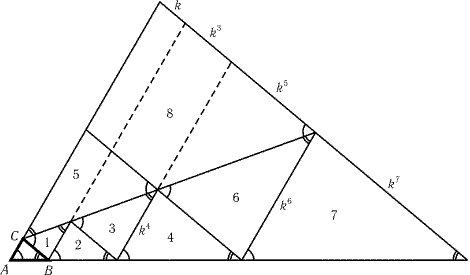
Как разбить треугольник на подобные ему треугольники? Очень легко разбить любой равносторонний треугольник на 4 равных равносторонних треугольника, соединив отрезками середины его сторон, то есть проведя средние линии рис. Продолжая разбивать этим же способом получающиеся части, мы сможем разделить исходный треугольник на 7, 10, 13, Отметим, что среди треугольников разбиения обязательно будут равные. Аналогично строится одна из самоподобных фигур — треугольник Серпинского такие фигуры называются фракталами. В равностороннем треугольнике проводятся средние линии и «вынимается» средний из четырёх получившихся треугольников.

Похожие статьи

• Поделка из бумаги треугольниками
• Как сделать в фотошопе прямоугольник с закругленными углами
• Диодная лента авто своими руками - Заземление в частном доме. Монтаж контура заземления
• Вязанные крючком игрушки и их схема